Quantum photonics with non-Hermitian systems

All physical systems can be roughly divided onto two types. Namely, conservative or Hermitian systems, where the whole system energy is preserved, and non-conservative or non-Hermitian systems, where the energy can irreversibly flow between the system and its surrounding environment.
Both types of systems can exhibit critical points (singularities) where the behavior of the system drastically changes, Both Hermitian and non-Hermitian systems can possess spectral singularities, called diabolic (DPs) and exceptional points (EPs), respectively. The main distinction between these two singularities is that while at a DP only system frequencies coalesce while eigenvectors remain orthogonal, at an EP both system frequency and its eigenmodes collapse. In other words, at DPs the system dimensionality is preserved, and at EPs it is necessarily reduced. The latter fact can lead to various nontrivial phenomena which have no counterparts in Hermitian systems, e.g., unidirectional light propagation, single-mode lasing, or extreme spectral sensitivity to name a few.
In previous works, however, the properties of DPs and EPs have been always investigated separately. In a recent study published in Nature Communications researchers from Joint Laboratory of Optics in Olomouc, in collaboration with their colleagues from Poland, Switzerland, USA and Japan, for the first time have theoretically demonstrated that, by simultaneously harvesting features of both EPs and DPs, one can realize a universal programmable photonic multimode switch. Namely, by specifically choosing dynamical trajectories in a system parameter space, which involve simultaneous encirclement of EPs and crossing DPs, it is possible to swap between any two system modes at will (as shown in Fig. 1 below). The most striking feature of such a switch is that one can choose between chiral and/or symmetrical mode switching regimes in a controllable fashion, which is unfeasible when relying solely either on DPs or EPs alone. The presented results thus open new perspectives for light manipulations in multimode systems which can be utilized for the development of novel photonic computing and communication protocols in both classical and quantum domain.
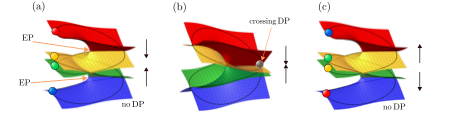
Fig 1. Programmable multimode switch: Encircling exceptional points (EPs), by crossing a diabolic point (DP) in a four-mode system. The vertical axis in all panels is the real-valued energy Re(E). (a) The four colorful balls represent system eigenmodes at initial time t=0. The initial state is characterized by two separated exceptional points, EPs (shown by orange arrows). At one of the EPs there is branch cut between the red and yellow Riemann sheets, and at the other EP there is a branch cut between the green and blue sheets. (b) When the encircling trajectory crosses the DP at the half period (shown by the grey ball), the four various energy Riemann sheets becomes connected. The presence of a DP is indicated by the intersection of two pairs of planes (the red and yellow sheets, and the green and blue sheets). (c) Final state at t = T: the eigenmodes are permuted compared to the initial modes, and that mode switching can be induced in a controllable manner.
I. Arkhipov, A. Miranowicz, F. Minganti, S. K. Ozdemir, and F. Nori, Nat. Commun. 14, 2076 (2023).



